Perspective Projection
Raycasting from Screenspace to World Coordinate in Perspective Camera Projection.
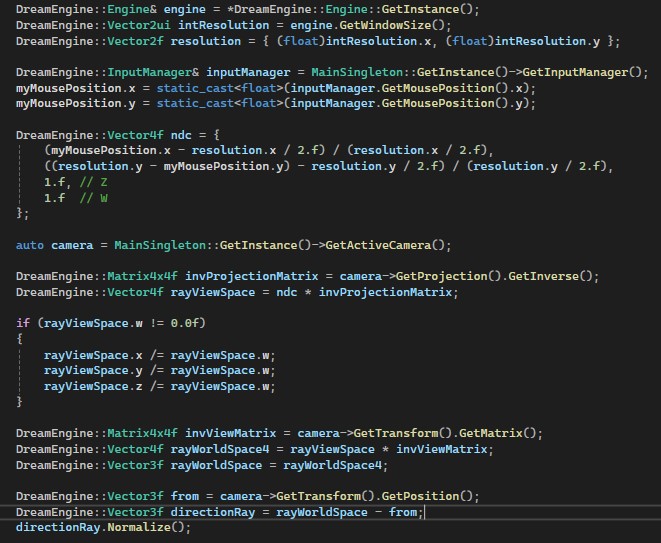
Step-by-Step Explanation
What we need to do is the inverse of the standard transformation from local space to screen space — following those steps in reverse.
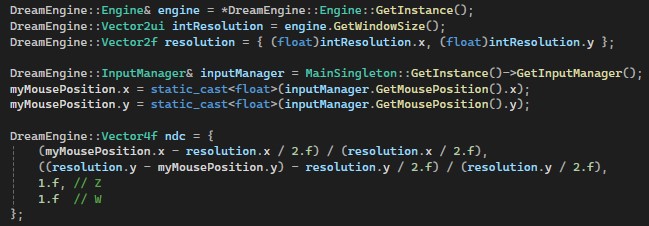
Firstly, we need the correct window size and mouse position. We convert the mouse position from screen space to Normalized Device Coordinates (NDC):
- -1 = left/bottom of the screen
- 1 = right/top of the screen
The Z-value is set to 1.0f,
assuming the ray starts from the far plane in clip space.
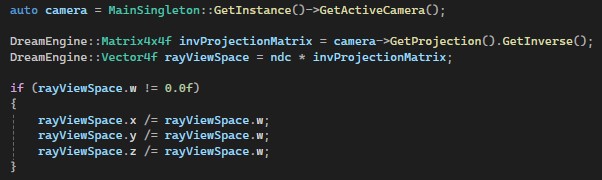
We retrieve the active camera to get its
projection matrix. This matrix is then
inverted to transform our NDC coordinates
into view space. Multiplying
ndc * invProjectionMatrix gives us the ray
direction in view space.
Since this uses homogeneous coordinates, we divide by the
w-component to normalize the result.
Next, we use the inverse view matrix from the camera to convert the ray from view space to world space. The resulting vector is a 4D position, but we only use its x, y, z components.
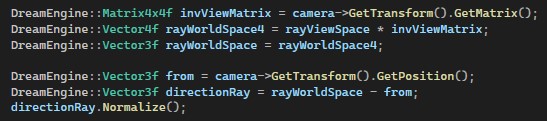
The origin of the ray is the camera's
position.
The direction is calculated by subtracting
the camera position from the transformed world-space ray
position and then normalizing the result.
Once this is retrieved, we can use it to raycast into the world.
Orthographic Projection
Raycasting from Screenspace to World Coordinate in Orthographic Camera Projection.

Explanation

Raycasting in
Orthographic Projection simplifies
calculations because the
near and far planes are the same size.
Unlike perspective projection:
- Objects remain the same size regardless of their distance from the camera.
- Rays do not converge but remain parallel.
The ray's direction is always the camera's forward vector, while the ray's origin is offset based on the calculated NDC values, ensuring it starts in the correct world space position.
